Introduction to quantum states
Quantum states, also known as wave functions, describe the condition of a quantum system. There are two main types of quantum states – pure states and mixed states. The key difference between them lies in whether the system can be described by a single wave function. Let’s explore this difference further.
There are two main types of quantum states:
What are pure quantum states?
Definition
A pure quantum state is one that can be described by a single wave function containing all the necessary information about the quantum system. Pure states represent systems where we have maximum knowledge – there is no uncertainty about the state of the system.
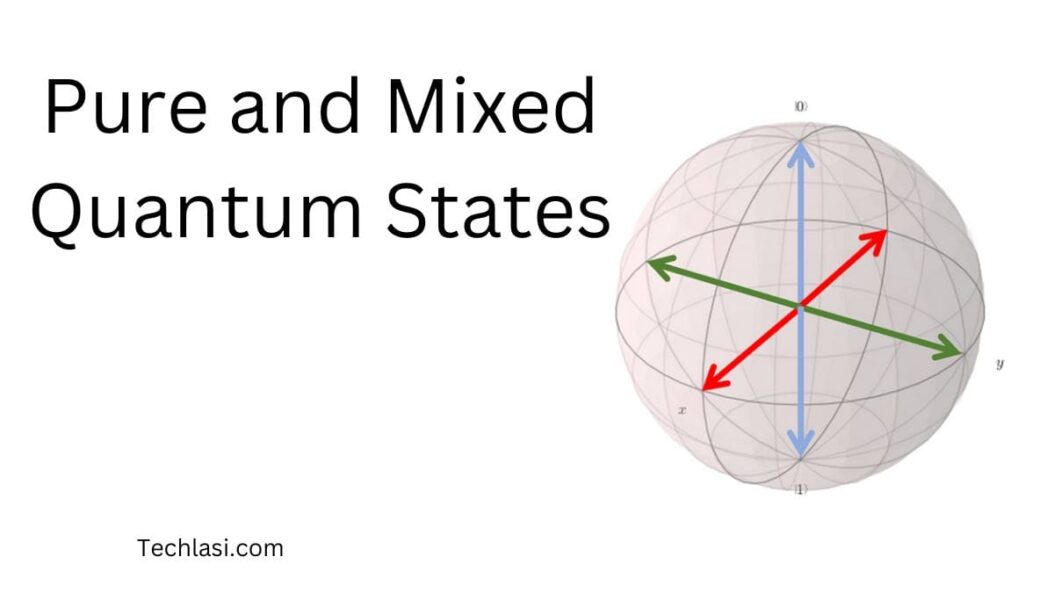
Mathematically, a pure state is described by a state vector $|\psi\rangle$ which can be visualized as a point on the surface of a sphere called the Bloch sphere. This representation captures all properties of the system accurately.
Characteristics
Some key traits of pure states:
- Single wave function description
- Maximum knowledge about quantum system
- Quantized energy levels
- Example: spin state of an electron
Representation
Pure states can be visually depicted as discrete points on the surface of the Bloch sphere, with each point corresponding to a unique state vector. This provides an intuitive way to distinguish pure states from mixed states.
Mixed quantum states
Definition
Mixed quantum states are represented by a statistical ensemble of multiple wave functions, instead of a single wave function. This ensemble captures the probability of the quantum system being in different configurations.
Mathematically, mixed states are described by a density matrix rho containing probabilities of different pure state configurations. The density matrix provides a more complete description for systems with uncertainty.
Characteristics
Properties of mixed states:
- Ensemble of multiple wave functions
- Partial knowledge about quantum system
- Non-quantized energy levels
- Example: photon polarization after measurement
Representation
Unlike pure states, mixed states correspond to interior points inside the Bloch sphere. The exact point depends on the probabilities of different configurations. This visually distinguishes mixed states from pure states on the surface.
Differences between pure and mixed states
Pure and mixed quantum states differ in some fundamental ways. The key differences include:
| Characteristic | Pure Quantum States | Mixed Quantum States |
| Certainty | Certain and deterministic | Involves uncertainty or lack of complete information |
| Representation | State vector in Hilbert space | Density matrix in Hilbert space |
| Quantum Properties | Associated with specific properties | Statistical mixture of properties from various pure states |
| Mathematical Formalism | Represented by a normalized state vector | Represented by a density matrix |
1. Knowledge about the system
Pure states provide maximal information about a quantum system its properties are completely defined. In contrast, mixed states have partial or incomplete information. The system could be in one of several quantum states.
2. Quantum coherence
Pure states exhibit full quantum coherence and can display interference effects. Mixed states have partial or no coherence between the constituent quantum states. This results in decoherence phenomena such as the loss of interference patterns.
3. Composition
Pure quantum states cannot be decomposed further into simpler states. Mixed states can always be decomposed into a statistical mixture of several pure states.
4. Preparation
Pure states correspond to perfectly isolated quantum systems. These are prepared through controlled interactions and are difficult to maintain due to decoherence effects.
Mixed states naturally occur when systems interact with the external environment. This leads to thermalization and loss of information about the system.
5. Dynamics
The time evolution of pure states is given by the fundamental Schrödinger equation. Mixed state dynamics also requires equations for the populations and coherences between constituent pure states.
6. Entanglement properties
Purely entangled quantum systems exist in a coherent superposition of basis states that cannot be factorized. Mixed state entanglement is weaker the system can usually be decomposed into statistical mixtures of non-entangled pure states.
Physical meaning of density matrix
- The density matrix ρ fully describes the statistical ensemble that makes up a mixed quantum state. What does each component physically mean?
- The diagonal elements ρii represent the population or probability of occupation of the pure state |ψi⟩ in the mixture.
- The off-diagonal elements ρij signify the amount of quantum coherence or interference between the pure state |ψi⟩ and |ψj⟩ in the ensemble.
- The trace Tr(ρ) gives the total probability to find the system in any one of the pure states making up the statistical ensemble. This must equal 1 for proper normalization.
- The number of non-zero eigenvalues of ρ gives the number of pure states in the mixture, a useful way to quantify mixedness.
Applications
The distinction between pure and mixed quantum states impacts many areas:
- Quantum computation: Maintaining pure states with long coherence times is essential for implementing qubits and quantum logic gates
- Quantum cryptography: Protocols like BB84 encode information in purely entangled photon states
Quantum measurements – Extracting information without inducing decoherence requires understanding and manipulating purity
- Quantum thermalization: Mixed states emerge from statistical mechanics of subsystems interacting with a large reservoir.
With growing interest in quantum technologies, understanding the difference between quantum reality (pure states) and the partial knowledge imposed by environmental interactions (mixed states) is increasingly important.
Conclusion
In summary, pure quantum states provide maximal knowledge and coherence while mixed states have partial information and lose that purely quantum behavior. This crucial difference emerges from interactions between the system and environment, and has profound consequences for quantum dynamics, entanglement and information processing. As we architect the second quantum revolution, harnessing the full potential of pure states while mitigating sources of decoherence poses an exciting challenge at the frontier of physics.
FAQs
Can a pure quantum state change into a mixed state over time?
Yes, interactions with the environment can cause initially pure states to become mixed over time through the process of decoherence, resulting in decaying quantum coherence. This effect places practical limits on harnessing pure states.
Are there any physical systems that can permanently remain in a pure state?
It is very difficult for macroscopic systems with many degrees of freedom to remain purely isolated from external interactions. However, simple few-particle quantum systems at extremely low temperatures can approach pure state behavior.
What kind of information is lost or gained when pure states become mixed?
The phase information between quantum states that encodes interference effects and correlations is rapidly lost in the decoherence process. However statistical information about the probabilities of different states remains robust.
What are the current methods used to protect pure quantum states from decoherence?
Quantum error correction codes, quantum computers operated at extremely low temperatures, and entangled states stored in quantum memories can protect valuable coherent quantum information.
How are highly mixed states different from classical statistical mixtures?
Highly mixed states still retain inherently quantum properties like entanglement which have no classical counterpart. But as decoherence increases, the behavior approaches that of probabilistic classical systems.
- How to Use and Access Claude 3: Pricing, Features, and Everything You Need to Know - March 5, 2024
- How AI is Revolutionizing Strategy Analysis? 2024 - March 1, 2024
- How AI is Transforming the Business of Advertising? - March 1, 2024